Given a set of coins and a total money amount. Write a method to compute the smallest number of coins to make up the given amount. If the amount cannot be made up by any combination of the given coins, return -1.
For example:
Given [2, 5, 10] and amount=6, the method should return -1.
Given [1, 2, 5] and amount=7, the method should return 2.
Java Solution 1 – Dynamic Programming (Looking Backward)
The solution one use a 2-D array for DP. If we look at the previous amount column value that is used in later amount column, the later column only cares about the minimum value of the previous column. Therefore, we can use a 1-D array instead of the 2-D array.
Given an amount of 6 and coins [1,2,5], we can look backward in the dp array.

Let dp[i] to be the minimum number of coins required to get the amount i.
dp[i] = 1, if i==coin
otherwise, dp[i]=min(dp[i-coin]+1, dp[i]) if dp[i-coin] is reachable.
We initially set dp[i] to be MAX_VALUE.
public int coinChange(int[] coins, int amount) { if(amount==0){ return 0; } int[] dp = new int[amount+1]; Arrays.fill(dp, Integer.MAX_VALUE); dp[0]=0; for(int i=1; i<=amount; i++){ for(int coin: coins){ if(i==coin){ dp[i]=1; }else if(i>coin){ if(dp[i-coin]==Integer.MAX_VALUE){ continue; } dp[i]=Math.min(dp[i-coin]+1, dp[i]); } } } if(dp[amount]==Integer.MAX_VALUE){ return -1; } return dp[amount]; } |
Time complexity is O(amount * num_of_coins) and space complexity is O(amount).
Java Solution 2 – Dynamic Programming (Looking Forward)
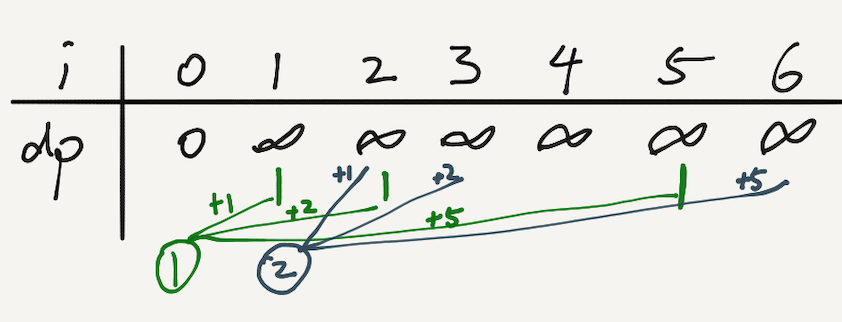
Let dp[i] to be the minimum number of coins required to get the amount i.
dp[i+coin] = min(dp[i+coin], dp[i]+1) if dp[i] is reachable.
dp[i+coin] = dp[i+coin] is dp[i] is not reachable.
We initially set dp[i] to be MAX_VALUE.
Here is the Java code:
public int coinChange(int[] coins, int amount) { if(amount==0){ return 0; } int[] dp = new int[amount+1]; Arrays.fill(dp, Integer.MAX_VALUE); dp[0]=0; for(int i=0; i<=amount; i++){ if(dp[i]==Integer.MAX_VALUE){ continue; } for(int coin: coins){ if(i<=amount-coin){ //handle case when coin is Integer.MAX_VALUE dp[i+coin] = Math.min(dp[i]+1, dp[i+coin]); } } } if(dp[amount]==Integer.MAX_VALUE){ return -1; } return dp[amount]; } |
Time and space are the same as Solution 1.
Java Solution 3 – Breath First Search (BFS)
Dynamic programming problems can often be solved by using BFS.
We can view this problem as going to a target position with steps that are allowed in the array coins. We maintain two queues: one of the amount so far and the other for the minimal steps. The time is too much because of the contains method take n and total time is O(n^3).
public int coinChange(int[] coins, int amount) { if (amount == 0) return 0; LinkedList<Integer> amountQueue = new LinkedList<Integer>(); LinkedList<Integer> stepQueue = new LinkedList<Integer>(); // to get 0, 0 step is required amountQueue.offer(0); stepQueue.offer(0); while (amountQueue.size() > 0) { int temp = amountQueue.poll(); int step = stepQueue.poll(); if (temp == amount) return step; for (int coin : coins) { if (temp > amount) { continue; } else { if (!amountQueue.contains(temp + coin)) { amountQueue.offer(temp + coin); stepQueue.offer(step + 1); } } } } return -1; } |
# The time is too much because of the contains method take n and total time is O(n^3).
———
what?? where did n^3 come from?
per each step moeny amount 1..N we add k coins. solutions.
#1 obv we need to mark already added amount to not repeat.
#2 no need 2 queue.
we can jsut keep #step inside amount : amount + max_amount(+1)*step, or just post fake sum (negative) into queue to count steps.
In case [2, 5, 10] and target 6, answer will be 3 by following solution.
public static int coinChange(int[] denom, int amount) {
List result = new ArrayList();
if (denom.length == 0 || amount == 0) {
return 0;
}
for (int i = denom.length - 1; i >= 0; i--) {
int d = denom[i];
while (amount >= d) {
amount -= d;
result.add(d);
}
}
return result.size();
}
I wrote a code using a dividing and mod operations and in one loop. but it will work onli in case when one of coins is equals 1.
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class CoinsMinimumNumber {
public static int findMinimumNumberOfCoins(int[] coins, int amount) {
int result = 0;
int remain = amount;
Arrays.sort(coins);
// I try to check the coins from big value to small value to find a minimum numbers of coins
int count = 0;
for (int i = coins.length -1; i >=0; i--) {
if (coins[i] <= remain) {
count = remain / coins[i];
result +=count;
if (remain % coins[i] == 0) {
break;
} else {
remain %= coins[i];
}
}
}
return result;
}
private static Integer coinChange2(int[] coins, int target) {
int max = target + 1;
int dp[] = new int[max];
Arrays.fill(dp, max);
dp[0] = 0;
for (int i = 0; i <= target; i++) {
for (int coin : coins) {
if (coin <= i) {
dp[i] = Math.min(dp[i], dp[i – coin] + 1);
}
}
}
return dp[target] == max ? -1 : dp[target];
}
A cleaner loop:
int [] f = new int[amount+1];
for (int i=1; i<=amount; i++) {
f[i] = Integer.MAX_VALUE;
}
for (int i=1; i= coin) {
if (f[i-coin] != Integer.MAX_VALUE) {
f[i] = Math.min(f[i], 1 + f[i-coin]);
}
}
}
}
if (f[amount] == Integer.MAX_VALUE) {
return -1;
}
return f[amount];
“Most dynamic programming problems can be solved by using BFS.” [citation needed]
The first solution should take O(k*n), where k is the amount and n is the number of denominations (2 nested loops)