LeetCode – Find Median from Data Stream (Java)

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Analysis

First of all, it seems that the best time complexity we can get for this problem is O(log(n)) of add() and O(1) of getMedian(). This data structure seems highly likely to be a tree.

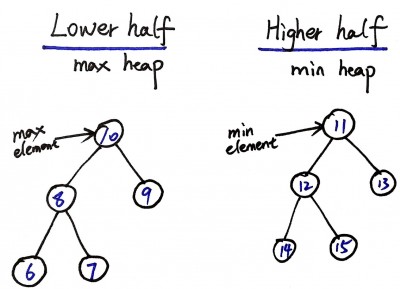
We can use heap to solve this problem. In Java, the PriorityQueue class is a priority heap. We can use two heaps to store the lower half and the higher half of the data stream. The size of the two heaps differs at most 1.

find-median-from-stream

class MedianFinder {
    PriorityQueue<Integer> minHeap = null;
    PriorityQueue<Integer> maxHeap = null;
 
    /** initialize your data structure here. */
    public MedianFinder() {
        minHeap = new PriorityQueue<>();
        maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
    }
 
    public void addNum(int num) {
        minHeap.offer(num);
        maxHeap.offer(minHeap.poll());
 
        if(minHeap.size()<maxHeap.size()){
            minHeap.offer(maxHeap.poll());
        }
    }
 
    public double findMedian() {
        if(minHeap.size() > maxHeap.size()){
            return minHeap.peek();
        }else {
            return (minHeap.peek()+maxHeap.peek())/2.0;
        }
    }
}

Category >> Algorithms

If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:

<pre><code> 
String foo = "bar";
</code></pre>

Gautam Tyagi

//https://gist.github.com/Vedrana/3675434
Mathias Haugsbø

Welll….. The median of [2,5,8,28] is 6.5 so the code is correct…. This is not to find average
Arif Azim

The above code does not offer correct median of stream of numbers –
Here it goes –

import java.util.PriorityQueue; import java.util.*;
public class Main { static PriorityQueue minHeap = new PriorityQueue(); static PriorityQueue maxHeap = new PriorityQueue(Collections.reverseOrder()); static int numberOfElements = 0; public static void addNum(int num){ maxHeap.add(num); if (numberOfElements%2 == 0) { if (minHeap.isEmpty()) { numberOfElements++; return; } else if (maxHeap.peek() > minHeap.peek()) { Integer maxHeapRoot = maxHeap.poll(); Integer minHeapRoot = minHeap.poll(); maxHeap.add(minHeapRoot); minHeap.add(maxHeapRoot); } } else { minHeap.add(maxHeap.poll()); } numberOfElements++; } public static Double findMedian(){ if (numberOfElements%2 != 0) return new Double(maxHeap.peek()); else return (maxHeap.peek() + minHeap.peek()) / 2.0; } public static void main(String[] args) { addNum(2); addNum(5); addNum(8); addNum(28);
System.out.println("Median " + findMedian()); } }

Output – 6.5
Anju rawat

very easy and clean code really appreciate that
Deepak Singh

Nice Solution
Sonali Vishwakarma

Very similar to the above solution, but much more intuitive. It actually also ran faster.

class MedianFinder {
PriorityQueue maxHeap;//lower half
PriorityQueue minHeap;//higher half

public MedianFinder(){
// Basically Collections.reverseOrder() makes your PriorityQueue a “maxHeap”. Otherwise, its a minHeap by default.
maxHeap = new PriorityQueue(Collections.reverseOrder());
minHeap = new PriorityQueue();
}

// Adds a number into the data structure.
public void addNum(int num) {
double median = 0;

// If there are no elements in maxHeap or minHeap, num is the median
if (maxHeap.size() == 0 && minHeap.size() == 0) {
median = (double) num;
}
else {
median = findMedian();
}

// Balancing minHeap and maxHeap. They should either have equal number of elements or differ by a size of one.

// If num is less than or equal to median, we should be putting it in maxHeap.
if (num <= median) {
// If maxHeap size is lesser than or equal to minHeap size, put it in maxHeap.
if (maxHeap.size() <= minHeap.size()) {
maxHeap.offer(num);
}
// If maxHeap size is greater than minHeap size, make some room in maxHeap,
// by removing the root from maxHeap and putting it in minHeap. Then,
// adding the num to maxHeap, since we made some room in the maxHeap.
else {
minHeap.offer(maxHeap.poll());
maxHeap.offer(num);
}
}
// If num is greater than median, we should be putting it in minHeap.
else {
// If minHeap size is lesser than or equal to maxHeap size, put it in minHeap.
if (minHeap.size() minHeap.size()) {
return (double) (maxHeap.peek());
} else {
return (double) (minHeap.peek());
}
}
}
anil

can someone xplain the logic behind this i mean how priority queue is used
Utkarsh Tiwari

I love this website 🙏🏻

LeetCode – Find Median from Data Stream (Java)

Related posts: