Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],…] find the minimum number of conference rooms required.
Java Solution
When a room is taken, the room can not be used for anther meeting until the current meeting is over. As soon as the current meeting is finished, the room can be used for another meeting. We can sort the meetings by start timestamps and sequentially assign each meeting to a room. Each time when we assign a room for a meeting, we check if any meeting is finished so that the room can be reused. In order to efficiently track the earliest ending meeting, we can use a min heap. Whenever an old meeting ends before a new meeting starts, we reuse the room (i.e., do not add more room). Otherwise, we need an extra room (i.e., add a room).
The time complexity is O(N*log(N)).
public int minMeetingRooms(int[][] intervals) { Arrays.sort(intervals, Comparator.comparing((int[] itv) -> itv[0])); PriorityQueue<Integer> heap = new PriorityQueue<>(); int count = 0; for (int[] itv : intervals) { if (heap.isEmpty()) { count++; heap.offer(itv[1]); } else { if (itv[0] >= heap.peek()) { heap.poll(); } else { count++; } heap.offer(itv[1]); } } return count; } |
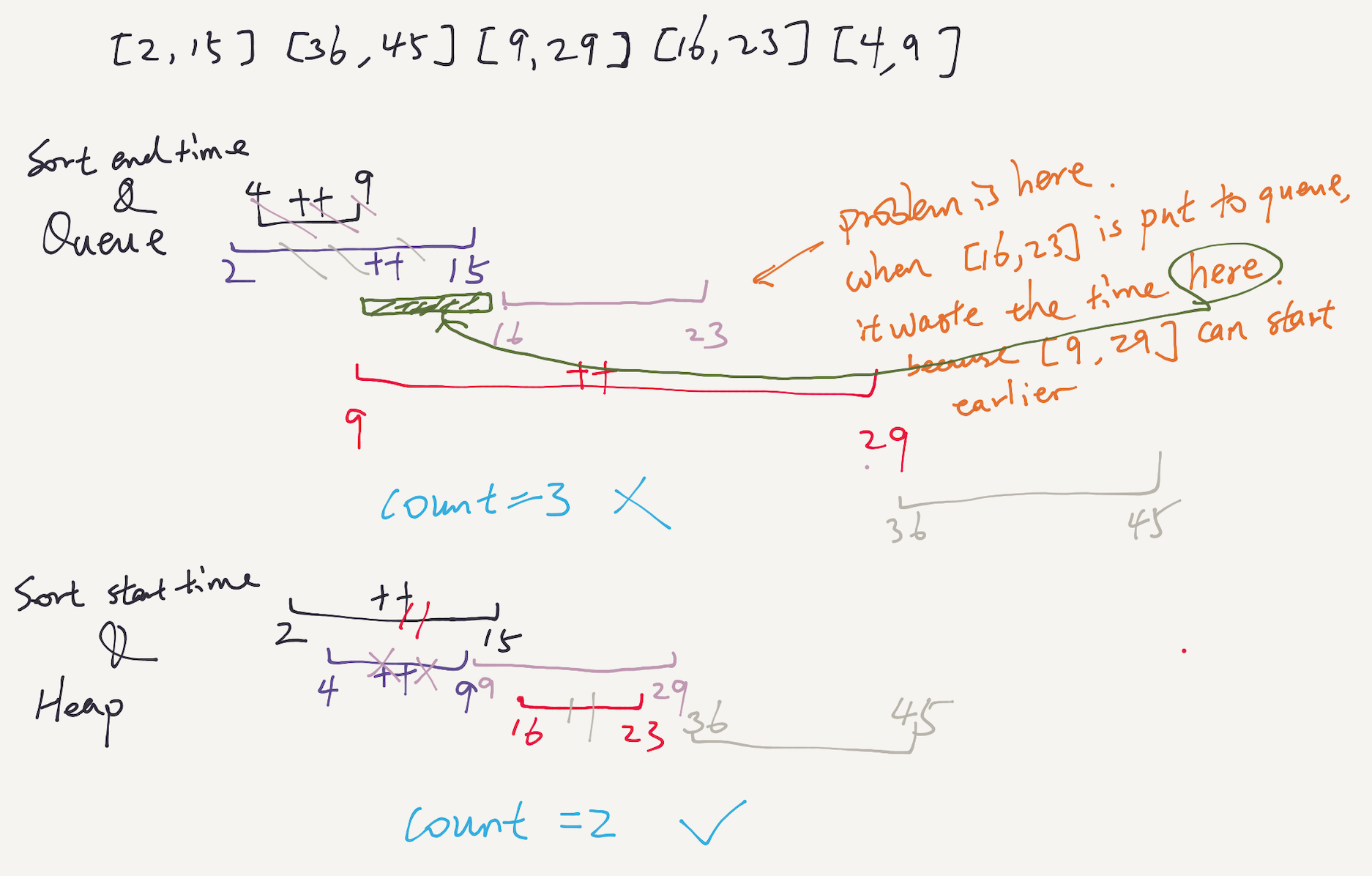
There was a discussion in the comments about why a regular queue is not good enough. I draw an example below to show why sorting based on start time and using a priority queue is necessary.
same hotel rooms reservations, only in this case we need 1 day per bucket, i guess
overall – 365
obv no need sorting or heap!
jsut do bucket sort(N) per minimal interval start:end
———
lets say timestamp is per hour 2:3, 4:5 , 12:18… etc
so allocate 1..24 buckets
add all intervals, start add1, finish subtract 1 , per hour bucket.
than just find max element in bucket, it will be minimal required
——-
this example
adding 1 : 2 4 9 16 36
subrract 1: 9 15 23 29 45
obv per 9 hour, we need 2 rooms , as it is max counter.
A simple solution would be to use two arrays: start times and end times. Sort them independently. Now keep two pointers to iterate over them. If start time comes first, that means one meeting has started so we need new room, while if end time comes first, that means one meeting is ended so we need lesser room now. The maximum of number of rooms needed at any time would be the answer (kind of similar to Kadane’s algorithm).
public int minMeetingRooms(List intervals) {
// Write your code here
int n = intervals.size();
List starts = new ArrayList();
List ends = new ArrayList();
for(Interval x : intervals) {
starts.add(x.start);
ends.add(x.end);
}
Collections.sort(starts);
Collections.sort(ends);
int i = 0, j = 0, current = 0, result = 0;
while(i < n) { // since last of ends would be greater than last of starts
// hence i will reach to end before ends, so no need to check j < n
if(starts.get(i) result ? current : result; // Update result
i++;
} else {
current--; // One meeting room is emptied, so need lesser meeting rooms now
// No need to update result here because we only want to maximize result
j++;
}
}
return result;
}
My solution in C# using a BST (it has a time complexity of O(N log N) with a space complexity of O(N)):
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Whiteboard
{
class MeetingRooms
{
private class Node
{
public int time;
public int offset;
public Node left;
public Node right;
public Node(int time, int offset)
{
this.time = time;
this.offset = offset;
this.left = null;
this.right = null;
}
}
public static void Run()
{
int[][] meetings = new int[][] { new int[] { 1100, 1200 }, new int[] { 1130, 1230 }, new int[] { 1200, 1230 } };
Console.WriteLine(GetMaxMeetingRooms(meetings));
}
private static int GetMaxMeetingRooms(int[][] meetings)
{
Node root;
int max = 0;
root = BuildBST(meetings);
max = GetMaxRooms(root);
return max;
}
private static Node BuildBST(int[][] meetings)
{
Node root = null;
foreach (int[] times in meetings)
{
int start = times[0];
int end = times[1];
AddTimeToTree(ref root, start, 1);
AddTimeToTree(ref root, end, -1);
}
return root;
}
private static void AddTimeToTree(ref Node node, int time, int offset)
{
if (node == null)
{
node = new Node(time, offset);
return;
}
if (time < node.time)
{
AddTimeToTree(ref node.left, time, offset);
}
else
{
AddTimeToTree(ref node.right, time, offset);
}
}
private static int GetMaxRooms(Node root)
{
int count = 0;
int max = 0;
_GetMaxRooms(root, ref count, ref max);
return max;
}
private static void _GetMaxRooms(Node node, ref int count, ref int max)
{
if (node == null)
{
return;
}
_GetMaxRooms(node.left, ref count, ref max);
count = count + node.offset;
max = Math.Max(count, max);
_GetMaxRooms(node.right, ref count, ref max);
}
}
}
Not working for below case
[[6,15],[13,20],[6,17]]
Expected: 3
OP: 1
//Program is similar to this but start and end meeting time are in different arrays
// Program to find minimum number of rooms
import java.util.*;
class MeetingRoom {
// Returns minimum number of rooms required
static int findMeetingRooms(int arr[], int dep[], int n)
{
// Sort start and departure arrays
Arrays.sort(arr);
Arrays.sort(dep);
// room_needed indicates number of rooms
// needed at a time
int room_needed = 1, result = 1;
int i = 1, j = 0;
// Similar to merge in merge sort to process
// all events in sorted order
while (i < n && j < n)
{
// If next event in sorted order is start time,
// increment count of rooms needed
if (arr[i] result)
result = room_needed;
}
// Else decrement count of rooms needed
else
{
room_needed–;
j++;
}
}
return result;
}
// Driver program to test methods of graph class
public static void main(String[] args)
{
int arr[] = {900, 940, 950, 1100, 1500, 1800};
int dep[] = {910, 1200, 1120, 1130, 1900, 2000};
int n = arr.length;
System.out.println(“Minimum Number of Rooms Required = ”
+ findMeetingRooms(arr, dep, n));
}
}
Why can’t we follow meeting room one soln ? like if there is an overlap then inc count then no extra space is required
Hey, thanks for a detailed solution.
Can you also explain how did you come up with this solution? thanks.
A JavaScript Solution:
Chinese: https://youtu.be/uEGNNeiMxuI
English: https://youtu.be/24li7yc91us
Youtube Channel: youtube.com/c/CatRacketCode
Facebook: https://www.facebook.com/groups/2094071194216385/
what about 0-2,0-4,0-5,7-8
It is showing extra count
answer should be 3 instead it is 4
What would be the runtime (big O) of your approach?
You don’t require a counter, heap size at the end is the required number of rooms
It is fine. Output is one meeting room.
Hi , i got a doubt. Whenever we are taking a new interval, instead of comparing with the smallest ending times why can’t we start comparing from largest of the finished ending times until we get a ending time which is smaller than current interval start time .
Example : priority Queue : {13,16}
Current interval : [17,21]
If we choose 16 -> priority queue :{16,17}
So here instead of 13 if we choose 16 -> priority queue : {13,17}
Isn’t the second case better than first one as it will give less collisions compared to first one.
I don’t think your solution is right. Try this example [[7,10],[2,4]]
public static int meetingRooms(Interval[] intervals) {
if (intervals.length == 0) {
return 0;
}
// Sort start of interval in ascending order
Arrays.sort(intervals, new Comparator() {
public int compare(Interval o1, Interval o2) {
return o1.start - o2.start;
}
});
int result = intervals.length; // Worst case all room will need its own room
for (int i = 0; i = intervals[i + 1].start // curr overlap with next
|| (intervals[i].start >= intervals[i + 1].start && intervals[i].end <= intervals[i + 1].end) // curr completely overlap with next
) {
result--;
}
}
return result;
}
why wont it?
It will work.
First 10-16 is compared with 11-13… count is incremented
then 11-13 is added to priority queue..
then 11-13 is compared with 14-17… count is NOT incremented.
Result: 2
this will not work for 10-16,11-13,14-17
No need for Priority Queue here, Simple solution here:
https://github.com/ankit249/Algorithms/blob/master/src/com/ds/basic/MeetingRooms.java
Instead of Priority Queue take simple queue to store elements but just sort by endTime .
private static int minMeetingRoomsQueue(Interval[] inte) {
int c = 0;
Arrays.sort(inte,new Comparator(){
@Override
public int compare(Interval o1, Interval o2) {
return o1.eTime - o2.eTime;
}
});
Queue q = new LinkedList();
q.add(inte[0].eTime);
c++;
for(int i=1;i<inte.length;i++){
if(inte[i].sTime < q.peek()){
c++;
}else{
q.poll();
}
q.add(inte[i].eTime);
}
return c;
}