Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
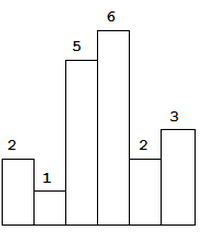
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
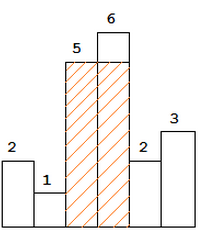
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example, given height = [2,1,5,6,2,3], return 10.
Analysis
If a bar is blocked by a lower bar, then the taller bar is no need to be considered any more. We only need to keep track of the bars that are not blocked. As we iterate over the bars, whenever a bar blocks a previous bar, we calculate how much area the previous bar can support.
The key to solve this problem is to maintain a stack to store bars’ indexes. The stack only keeps the increasing bars.
Java Solution
public int largestRectangleArea(int[] height) { if (height == null || height.length == 0) { return 0; } Stack<Integer> stack = new Stack<Integer>(); int max = 0; int i = 0; while (i < height.length) { //push index to stack when the current height is larger than the previous one if (stack.isEmpty() || height[i] >= height[stack.peek()]) { stack.push(i); i++; } else { //calculate max value when the current height is less than the previous one int p = stack.pop(); int h = height[p]; int w = stack.isEmpty() ? i : i - stack.peek() - 1; max = Math.max(h * w, max); } } while (!stack.isEmpty()) { int p = stack.pop(); int h = height[p]; int w = stack.isEmpty() ? i : i - stack.peek() - 1; max = Math.max(h * w, max); } return max; } |
This does not work for an increasingly sorted array. Say 3,4,5,6,7.
public static int largestRectArea(int[] height) {
int max = 0;
if (height.length == 0 || height == null) {
return 0;
}
int i = 0;
while (i = 0) {
if (height[j] < h) {
h = height[j];
max = Math.max(height[j] * (i – j + 1), max);
} else {
max = Math.max(h * (i – j + 1), max);
}
j–;
}
i++;
}
return max;
}
nice explanation!!
I’m reasoning out this way. Does this make sense?
I’ll maintain a stack of blocks that are in the increasing order. Once I see that a block comes my way that is smaller than the latest block that I have seen so far, I know that the rectangle that can be formed by the last block can’t be extended beyond that one anymore. So, I’ll go and process the contents of the stack to find out what’s the max area that can be obtained by the blocks that are a part of the stack so far.
Once I’ve processed those blocks, I know what’s the max area rectangle that’s supported by those blocks. And now I’ll start working from the block that I have just seen by adding it to the stack and continue repeating the process.
Once I have reached the end of the array of blocks, I know that there will be at least one block that’s not processed. So I’ll process that one as well and any others that are still in the stack.
Now the way I process the blocks to calculate the max area rectangle is as below:
I know that the top element in the stack is taller than where I’m right now (i). So I’ll calculate the area that’s supported by that one. I know it’s height (arr[stack.pop()]), but I need to calculate its width as well. The way it’s done is as below:
If the stack is not empty, it means that this block has started counting/mattering only recently, from some index onwards. So I’ll look at the stack’s top to get a sense of from when this block started counting/mattering for our calculations. And also note that I’ve moved one block further from this block who’s max area I want to calculate. So I need to reduce 1 from my current_location (which is i).
So my equation would be: (current_location – 1 – stack.peek())
If the stack is empty, I know that since the starting of the array the histogram has at least this height being supported. If not, I’d have had some entries in there from the past.
So in this case, the width would be: (current_location)
So overall, my width calculation would be: int width = stack.isEmpty() ? current_loc : current_loc – 1 – stack.peek()
My solution:
private static double solution(double[] hist) {
Stack pStack = new Stack(), hStack = new Stack();
double insertPos, cHeight, potMax, maxA = 0;
for (int i = 0; (insertPos = i) cHeight)
if ((potMax = (i - (insertPos = pStack.pop())) * hStack.pop()) >= maxA)
maxA = potMax;
if (hStack.isEmpty() || hStack.peek() != cHeight) {
pStack.push(insertPos);
hStack.push(cHeight);
}
}
return maxA;
}
int maxArea(int[] a) {
if (a == null || a.length == 0) {
return 0;
}
int max = 0;
for (int i = 0; i 0 && a[j] >= a[i]; j--) {
width++;
}
for (int j = i + 1; j = a[i]; j++) {
width++;
}
max = Math.max(max, a[i] * (width));
}
return max;
}
Does this work for 2,4,5,6,7? Wouldn’t it throw IndexOutOfBoundsException when you do height[7] in the second while loop, after you do stack.pop()?
Can someone explain how this works? The analysis behind it? Thanks. I came up with and n^2 time and constant space solution using the left, right approach but can’t grasp this proposed solution
yup, you can easily prove it’s not working by using something smallish, something bigger, something smallest… 🙂 like 2, 3, 1 is the simplest case.
This is a good solution, but still takes o(n^2) in the worse case: {1, 2, 4, 5, 6, 8, 10…}
int w = stack.isEmpty() ? i : i – stack.peek() – 1;
Why “-1”? Could someone tell me? Pls use [1 ,4 ,2] to walk through.
some observation:
maxLeft[i]: trace back from i to left, the first index with a value less than bar[i];
maxRight[i]: trace forward from i to right, the first index with a value than bar[i];
The max area around i: is bar[i]*( maxRight[i]-maxLeft[i]-1)
Test cases:
System.out.println(solution(new int[]{2,1,5,6,2,3}));
System.out.println(solution(new int[]{2,1,0,6,2,3}));
System.out.println(solution(new int[]{2,1,2,6,1,7,1,0,6,2,3}));
An O(N) solution via iteration using Dynamic Programming:
public static int solution(int[] bar) {
//parameter check
assert (bar != null && bar.length > 0);
//initialization
int[] maxLeft = new int[bar.length];
int[] maxRight = new int[bar.length];
maxLeft[0] = -1;
maxRight[bar.length-1] = bar.length;
int maxArea = -1;
//calculate maxLeft
for(int i = 1; i = 0) {
if (bar[i] > bar[leftCur]) {
break;
}
else {
leftCur = maxLeft[leftCur];
}
}
maxLeft[i] = leftCur;
}
//calculate maxRight
for(int i = bar.length-2; i >= 0; –i) {
int rightCur = i+1;
while(rightCur bar[rightCur]) {
break;
}
else {
rightCur = maxRight[rightCur];
}
}
maxRight[i] = rightCur;
}
//find max
for(int i = 0; i maxArea) maxArea = curSize;
}
return maxArea;
}
How is this O(n)?
You are making it too complicated. Here is simple solution for this problem:
public static int largestRectArea(int[] height) {
int max = 0;
if (height.length == 0 || height == null) {
return 0;
}
int i = 0;
while (i = 0) {
if (height[j] < h) {
h = height[j];
max = Math.max(height[j] * (i – j + 1), max);
} else {
max = Math.max(h * (i – j + 1), max);
}
j–;
}
i++;
}
return max;
}