LeetCode – Maximum Subarray (Java)

Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array [−2,1,−3,4,−1,2,1,−5,4], the contiguous subarray [4,−1,2,1] has the largest sum = 6.

Java Solution - DP

The easiest way to formulate the solution of this problem is using DP. Let f(n) be the maximum subarray for an array with n elements. We need to find the subproblem and the relation.

f(n) = { f(n-1)>0 ? f(n-1) : 0 } + nums[n-1]

f(0) = 0
f(1) = nums[0]

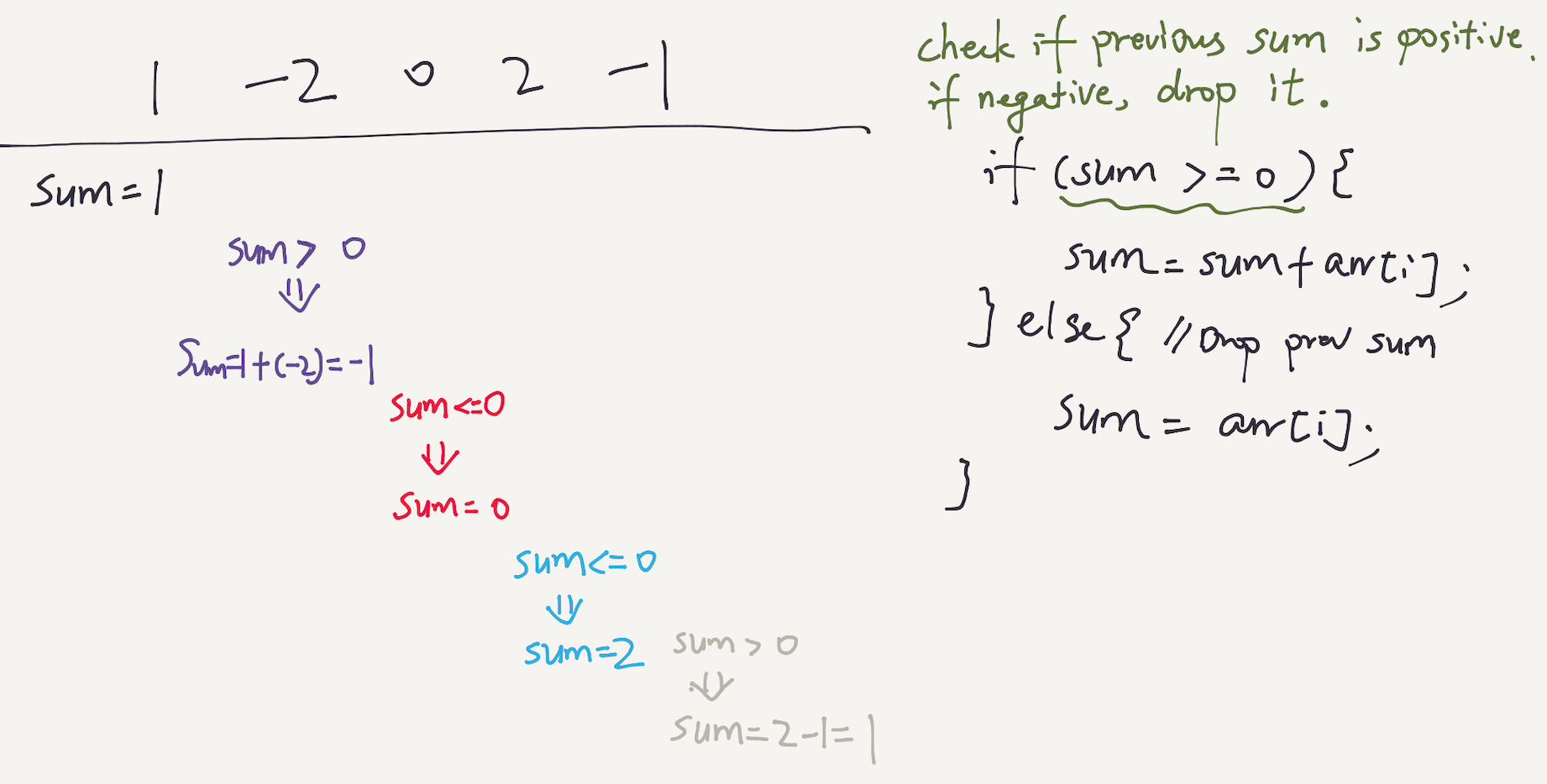
The changing condition for dynamic programming is "We should ignore the sum of the previous n-1 elements if nth element is greater than the sum."

public int maxSubArray(int[] nums) {
    int result = nums[0];
    int[] sum =  new int[nums.length];
    sum[0] = nums[0];
 
    for(int i=1; i<nums.length; i++){
        sum[i] = Math.max(nums[i], sum[i-1] + nums[i]);
        result = Math.max(result, sum[i]);
    }
 
    return result;
}

The time complexity and space complexity are the same O(n). However, we can improve the space complexity and make it to be O(1).

public int maxSubArray(int[] nums) {
    int result = nums[0];
    int sum = nums[0];
 
    for(int i=1; i<nums.length; i++){
        sum = Math.max(nums[i], sum + nums[i]);
        result = Math.max(result, sum);
    }
 
    return result;
}

Category >> Algorithms

If you want someone to read your code, please put the code inside <pre><code> and </code></pre> tags. For example:

<pre><code> 
String foo = "bar";
</code></pre>

Mo Hassanpour

for(int i=1; i sum[i-1] + A[i]) { //???
…
} else { //???
…
}
Mo Hassanpour

”
for(int i=1; i sum[i-1] + A[i]) {
”
???
Kaushlendra Singh

// modified to print the sub array containing maximum sum var start = 0, end = 0; var nums = [-2,1,-3,4,-1,2,1,-5,4]; var prevRes = 0; var result = nums[0]; var sum = nums[0]; for ( var i =1; i < nums.length ; i++) { if( sum <= 0){ sum = nums[i]; start = i; } else { sum += nums[i]; } prevRes = result; result = Math.max(result, sum); if(prevRes < result){ end = i console.log("i",i) } }
console.log(result) /*print the sub array containing maximum sum */ console.log(nums.slice(start,end+1))
Marina

Also there is an improvement of upper dynamic programming solution – you do not need array to store intermediate sums as we only need to know previous sum. This one is faster, and requires O(1) space
public int maxSubArray(int[] A) { int max = A[0]; int sum = A[0];
for (int i = 1; i < A.length; i++) { sum = Math.max(A[i], sum + A[i]); max = Math.max(max, sum); } return max;
}
Marina

this one was accepted at leetcode:
int maxSum = Integer.MIN_VALUE; if (A.length == 0) { return maxSum; } if (A.length == 1) { return A[0]; } for (int i = 0; i < A.length; i++) { int sum = 0; for (int j = i; j< A.length ; j++) { sum += A[j]; maxSum = Math.max(sum, maxSum); } } return maxSum;
Local Guy

The problem statement seems inaccurate. Rather than getting the subarray, you’re only supposed to get the sum.
Bandi Shankar

much clean solution would be

// input the position of element of array “a”
int maxSub(int pos){
if(pos == 0)
return a[0];
else{
return Math.max(maxSub(pos-1)+a[pos], a[pos]);
}
}
Thomas Mech

Could you please explain why the complexity is O(1) and not O(n)?
As I see it, the for loop is repeated n-1 times.
Norman Amos

This seems simpler:

public static int maxSubArray(int[] a) { int r = 0; int l = 0; int rsum = 0; int lsum = 0; int rmax = Integer.MIN_VALUE; int lmax = Integer.MIN_VALUE; for (int i = 0; i rmax) { rmax = rsum; r = i; } if (lsum > lmax) { lmax = lsum; l = a.length - i - 1; } } int rtn = rmax + lmax - rsum; System.out.println("a[" + l + "] + ... + a[" + r + "] = " + rtn); return rtn; }
Avinash Ujjwal

/* Here is the solution using kadane’s algorithm but it only works when there is at least one positive element in the given array. */

public static int maxSubArray(int[] array) {
int maxSum = 0, newSum = 0;

for(int i = 0; i 0) {
newSum = newSum + array[i];
} else {
newSum = 0;
}
maxSum = Math.max(maxSum, newSum);
}
return maxSum;
}
Mohan Gaddam

Guess it fails for lot of cases, For Ex input Array:
5, -4, 9, -3500, 25, -3, 12, 5900, 15, -23, 18, 14, 11, 93, 12, 34, 56, -125, 66, -255, 95, 68, 4558, -2, 203
Eric

only fails with all negative numbers
Prasad Kailkere Sridhar

Extending Mehdi’s solution, you can track the subarray (indices) using 2 more variables startIndex and endIndex (initialize before the for loop and add below code inside the for loop at the end):

if (max == A[i])
{
startIndex = i;
}
else if (max == newsum)
{
endIndex = i;
}
Allan Yin

I will still work. plz test yourself.
Dexter

Solution with array indexes:

public static void maxArray(int[] arr){

int prevStart = -1;

int currentStart = prevStart;

int maxHere = 0;

int maxSoFar = 0;

int end = -1;

for(int i = 0; i< arr.length; i++){

if(arr[i] < 0 && maxSoFar == 0){

continue;

}

maxHere += arr[i];

if(currentStart == -1){

currentStart = i;

}

if(maxHere maxSoFar){

maxSoFar = maxHere;

prevStart = currentStart;

end = i;

}

}

System.out.println(“Max Sum:” + maxSoFar);

System.out.println(“Start: ” + prevStart);

System.out.println(“End: ” + end);

}
Satish

Copy pasted from eclipse ide.I m not sure why it appears this way. Sorry for that
Satish

Check this out O(1) with position:

public static int maxSubArray(int[] A) {
int newsum=A[0];
int max=A[0];
int j = 0;
int i_max = 0;
for(int i=1; i<A.length; i++){
newsum += A[i];
if (newsum max) {
max = newsum;
i_max = i;
}
}
System.out.println(j + “,” + i_max + ” = ” + max);
return max;
}
Sam

The naive solution should work on {-1, -2, 5, -2}.
could you double check plz?
Stephen Boesch

The DP solution is not correct. The condition should be “we ignore the previous n-1 sum if it were less than or equal to 0”.
Dhwanit Shah

Above solution is not correct. Pls find the rectified complete solution below:

#include
using namespace std;
int max(int a, int b)

{
if(a>b)
return a;
return b;
}

int maxSubArray(int* A, int len) {

int sum = 0;
int maxSum = -1000000; //some very large negative number

for (int i = 0; i < len; i++) {
if (sum < 0){
sum = A[i]; // change
}
else
{
sum += A[i];
}
maxSum = max(maxSum, sum); // change
}
return maxSum;
}

int main() {
int a[] = {-1,-2,3,4,-5,6};
cout<<maxSubArray(a, 6);
return 0;
}
swm8023

The first solution is correct. It’s same to the last solution
ryanlr

Put code between <pre> and </pre>
garukun

Thanks! I was wondering how you guys created code like posting.
ryanlr

This solution is wrong, I tried it using { -1, -2, 5, -2 }.
ryanlr

I think your solution is also correct.
ryanlr

I have added this solution, thanks!
garukun

Will something like this work? We observe that the if the element about to be added to create the next summation is already greater than the previous summation, then we will ignore the previous summation and start a new maxSum from the current index. The code would look something like:

[code]

public int maxSum(int[] arr) {

int maxSum = Integer.MIN_VALUE;

for (int i = 0, sumSoFar = -1, sum; i sum) {

sumSoFar = arr[i];

} else {

sumSoFar = sum;

}

maxSum = Math.max(maxSum, sumSoFar);

}

return maxSum;

}

// Test input and iterations
[−2,1,−3,4,−1,2,1,−5,4]

i = 0; sum = -3, sumSoFar = -2, maxSum = -2 ;

i = 1; sum = -1, sumSoFar = -1, maxSum = -1 ;

i = 2; sum = -4, sumSoFar = -3, maxSum = -3 ;

i = 3; sum = 1, sumSoFar = 4, maxSum = 4 ;

i = 4; sum = 3, sumSoFar = 3, maxSum = 3 ;

i = 5; sum = 5, sumSoFar = 5, maxSum = 5 ;

i = 6; sum = 6, sumSoFar = 6, maxSum = 6 ;

i = 7; sum = 1, sumSoFar = 1, maxSum = 6 ;

i = 8; sum = 5, sumSoFar = 5, maxSum = 6 ;

[/code]
Kevin

An array with all negative number will break naive solution, since “(containing at least one number) “
Jiaming

The “Naive Solution” works, nothing’s wrong with that line, I think it’s not working anymore if you change that row.
Shaowei Ling

Based on the second method(DP style), I write this for printing the sub array in details. I tested the example in the question and it works.

public int maxSubArray(int[] A) {
int max = A[0];
int[] sum = new int[A.length];
sum[0] = A[0];

int begin = 0;
int end = 0;

for(int i=1; i sum[i-1] + A[i]) {
sum[i] = A[i];
newBegin = i;
newEnd = i;
} else {
sum[i] = sum[i-1] + A[i];
newEnd = i;
}

if(sum[i] > max) {
max = sum[i];
begin = newBegin;
end = newEnd;
}
}

// print the subArray
for(int i = begin; i <= end; i++) {
System.out.print(A[i]+ " ");
}
System.out.println();

return max;
}
play_boy

Native Solution is wrong, but you can change some row, and it will be ok!

like this:

public static int maxSubArray(int[] A) {
int sum = 0;
int maxSum = Integer.MIN_VALUE;

for (int i = 0; i < A.length; i++) {
sum += A[i];

if (sum < 0)
sum = A[i]; // change
maxSum = Math.max(maxSum, sum); // change
}

return maxSum;
}

Mehdi

you can also do it with O(1) space complexity instead of O(n):

  public int maxSubArray(int[] A) {
       int newsum=A[0];
       int max=A[0];
       for(int i=1;i<A.length;i++){
           newsum=Math.max(newsum+A[i],A[i]);
           max= Math.max(max, newsum);
       }
       return max;
    }

Yat

Hi, what about the actual subarray that should be returned? Only the max sum is returned in the two solutions above.
曹超

because it’s a wrong method
曹超

原理就是错的
Darren

Why does the so-called “Naive Solution” not work? I think the algorithm is correct, and it passes the OJ as well.

LeetCode – Maximum Subarray (Java)

Related posts: