A Java-based set of classification clustering algorithms. Built under JDK 1.7 and tested up to JDK 1.8. This project is currently in ongoing development for the time being and should not be used in production environments
clust4j 1.1.6 prerelease is now available under releases. To build the bleeding edge, use the included gradle wrapper:
git clone https://github.com/tgsmith61591/clust4j.git
cd clust4j
./gradlew build ## Go grab some coffee... this takes a minute
## jar is at build/libs/clust4j-x.x.x.jar and includes dependenciesGet started quickly with clust4j by loading one of the built-in datasets:
Usage:
DataSet data;
data = ExampleDataSets.loadIris();
data = ExampleDataSets.loadWine();
data = ExampleDataSets.loadBreastCancer();final int k = 2;
final Array2DRowRealMatrix mat = new Array2DRowRealMatrix(new double[][] {
new double[] {0.005, 0.182751, 0.1284},
new double[] {3.65816, 0.29518, 2.123316},
new double[] {4.1234, 0.2301, 1.8900002}
}); Partitional algorithms:
k-Means, an unsupervised clustering method that aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean (centroid), serving as a prototype of the cluster.
KMeans km = new KMeansParameters(k).fitNewModel(mat);
final int[] results = km.getLabels();k-Medoids, an unsupervised clustering method that chooses datapoints as centers (medoids or exemplars) and works with an arbitrary matrix of distances between datapoints instead of using the Euclidean norm.
KMedoids km = new KMedoidsParameters(k).fitNewModel(mat);
final int[] results = km.getLabels();Affinity Propagation, a clustering algorithm based on the concept of "message passing" between data points.Like KMedoids, Affinity Propagation finds "exemplars", members of the input set that are representative of clusters.
AffinityPropagation ap = new AffinityPropagationParameters().fitNewModel(mat);
final int[] results = ap.getLabels();Hierarchical algorithms:
HierarchicalAgglomerative, a "bottom up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy. Agglomerative clustering is not computationally friendly in how it scales. The agglomerative clustering procedure performs at O(n2), but far outperforms its cousin, Divisive Clustering.
HierarchicalAgglomerative a = new HierarchicalAgglomerativeParameters().fitNewModel(mat);
final int[] results = a.getLabels();Density-based algorithms:
DBSCAN, a density-based clustering algorithm: given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away).
DBSCAN db = new DBSCANParameters(0.75).fitNewModel(mat);
final int[] results = db.getLabels();HDBSCAN, a density-based clustering algorithm: performs DBSCAN over varying epsilon values and integrates the result to find a clustering that gives the best stability over epsilon. This implementation includes five algorithms: PrimsKD, PrimsBall, BoruvkaKD and BoruvkaBall.
HDBSCAN hdb = new HDBSCANParameters().fitNewModel(mat);
final int[] results = hdb.getLabels();MeanShift, a non-parametric feature-space analysis technique for locating the maxima of a density function, a so-called mode-seeking algorithm.
MeanShift ms = new MeanShiftParameters(0.5).fitNewModel(mat);
final int[] results = ms.getLabels();Neighbor point clustering algorithms:
NearestNeighbors, a neighbor clusterer that will fit the k-nearest points for each record in a matrix.
NearestNeighbors nn = new NearestNeighborsParameters(k).fitNewModel(mat);
Neighborhood neighborhood = nn.getNeighbors();
int[][] indices = neighborhood.getIndices(); // The indices in order of nearness
double[][] distances = neighborhood.getDistances(); // The corresponding distancesRadiusNeighbors, a neighbor clusterer that will fit the nearest points within a given radius.
RadiusNeighbors rn = new RadiusNeighborsParameters(1.5).fitNewModel(mat);
Neighborhood neighborhood = rn.getNeighbors();
int[][] indices = neighborhood.getIndices(); // The indices in order of nearness
double[][] distances = neighborhood.getDistances(); // The corresponding distancesSupervised clustering algorithms:
NearestCentroid, a supervised algorithm that fits centroids based on a set of observed labels.
NearestCentroid nc = new NearestCentroidParameters().fitNewModel(mat, new int[]{0,1,1});
// you can use .predict(AbstractRealMatrix) to retrieve predicted class labels on new dataAll clustering algorithms that implement Classifier can also be scored. Supervised and unsupervised methods are scored in different manners. If we want to score the NearestCentroid model we fit above:
// implicitly uses ground truth and predicted labels
double accuracy = nc.score();Conversely, if we'd like to score an unsupervised algorithm, we have a few options. Every UnsupervisedClassifier implements a silhouetteScore method, but also implements a home-grown scoring algorithm called INDEX_AFFINITY. This operates based on the following complication:
// our k-means model predicts labels like this:
km.getLabels(); // {0,1,1}
// ...but the ground truth may actually be {9,15,15}... this method, then, is an attempt to measure accuracy not traditionally, but by accounting for predicted segmentation in regards to actual label segmentation. It works by penalizing indices which are inappropriately associated with incorrect neighbor indices. In this regard a ground truth set of {0,1,0,2,2} and predicted set of {2,0,2,1,1} would be 100% accurate. Use as follows:
km.indexAffinityScore(new int[]{50,10,10}); // 100%Alternatively, the silhouetteScore method can be called as follows:
km.silhouetteScore(); // Uses internally predicted labelsAny algorithm implementing BaseClassifier or its sub-interfaces will implement the method predict(AbstractRealMatrix). After the model has been fit, predictions can be made as follows (using KMeans for example):
KMeans model = new KMeansParameters(2).fitNewModel(mat); // fit the model on the training data
Array2DRowRealMatrix newData = new Array2DRowRealMatrix(new double[][]{ // here's the new data
new double[]{0.0, 0.0, 0.0},
new double[]{3.0, 0.0, 2.0}
});
int[] predicted_labels = model.predict(newData); // returns {0, 1}Note that HDBSCAN does not currently implement a functional predict method, and will throw an UnsupportedOperationException.
TrainTestSplitclust4j includes a TrainTestSplit class that will shuffle and split a DataSet given a training ratio. This can be useful for both SupervisedClassifiers as well as UnsupervisedClassifiers (especially when leveraging clust4j's own proprietary INDEX_AFFINITY as a scoring metric). Here's an example of how this can be used with KMeans:
// Load data, get splits
TrainTestSplit split = new TrainTestSplit(ExampleDataSets.loadIris(), 0.70);
DataSet train = split.getTrain(), test = split.getTest();
// Fit a model and get predictions
KMeans model = new KMeansParameters(3).fitNewModel(train.getData());
int[] predicted_labels = model.predict(test.getData());
// Get the "affinity" score using the Index Affinity algorithm:
double affinity = ClassificationScoring.INDEX_AFFINITY.evaluate(test.getLabels(), predicted_labels)Pipeline:clust4j includes a Pipeline object to feed data through a series of ordered PreProcessors and finally, into a clustering model (see below, in the utilities section for more info). Here's an example:
// Let's predict whether a tumor is malignant or benign:
TrainTestSplit split = new TrainTestSplit(ExampleDataSets.loadBreastCancer(), 0.7);
// Get the splits
DataSet training = split.getTrain();
DataSet holdout = split.getTest();
// Initialize pipe
SupervisedPipeline<NearestCentroid> pipeline = new SupervisedPipeline<NearestCentroid>(
// This is the parameter class for the model that will be fit
new NearestCentroidParameters()
.setVerbose(true)
.setMetric(new GaussianKernel()),
// These are the preprocessors that will transform the training data:
new StandardScaler(), // first transformation
new MinMaxScaler(), // second transformation
new PCA(0.85) // final transformation
);
// Fit the pipeline:
pipeline.fit(training.getData(), training.getLabels());
// Make predictions:
int[] predicted_labels = pipeline.predict(holdout.getData());A number of separability metrics are available for use:
<x,y> plus an optional constant c.Notice the differentiation between similarity-based and distance-based geometrically separable metrics. All the clustering algorithms are able to handle any metric implementing the GeometricallySeparable interface. Since SimilarityMetric's getSimilarity(...) method should return the negative of getDistance(...), separability metrics implementing SimilarityMetric implicitly will attempt to maximize similarity (as all clustering algorithms will minimize distance). Classes implementing SimilarityMetric should define the getDistance(double[], double[]) method to return -getSimilarity(double[], double[]).
Various similarity metrics—kernel methods, in particular—allow the clustering algorithm to segment the data in Hilbert Space[4], which can—assuming the proper kernel is selected—allow the algorithm to identify "complex," or non-(hyper)spherically shaped clusters:
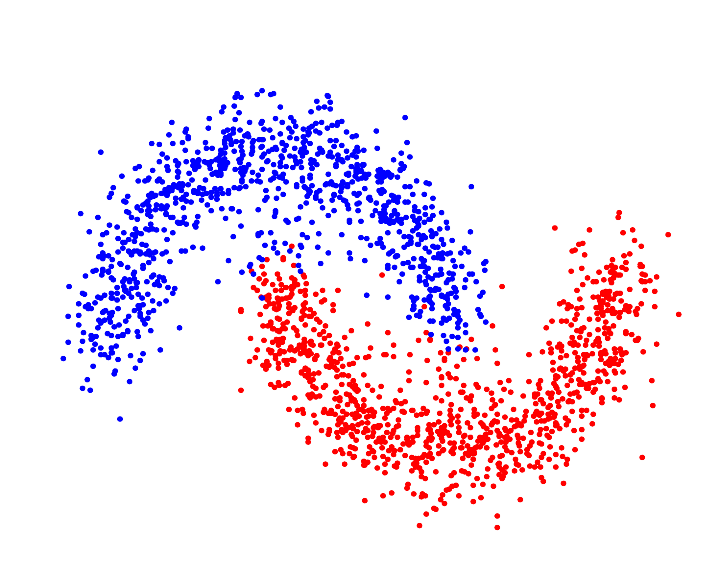
Whereas a distance metric in Euclidean space may struggle with oddly shaped clusters[9]:
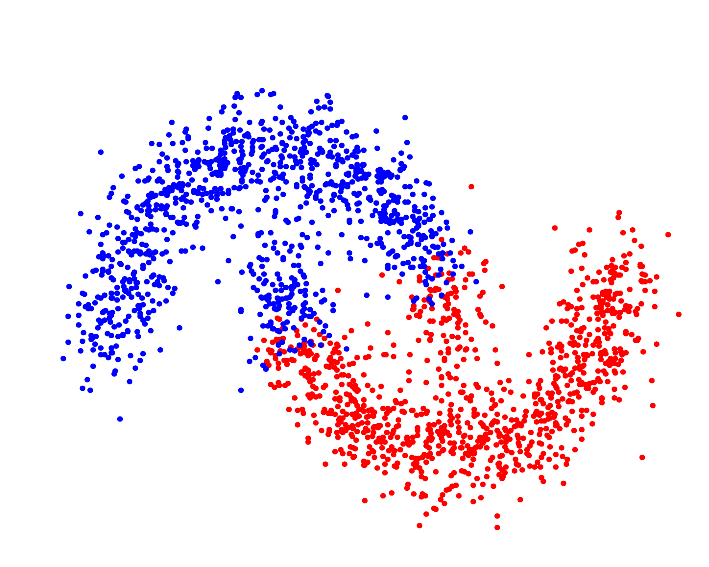
To initialize any clusterer with a kernel as the GeometricallySeparable metric (example uses GaussianKernel):
final Kernel kernel = new GaussianKernel();
KMedoids km = new KMedoids(mat, new KMedoidsPlanner(k).setSep(kernel));Note: though similarity metrics may be used with any clustering algorithm, it is recommended that they not be used with density-based clustering algorithms, as they seek "neighborhoods" around points and similarity metrics such as kernels will not accurately describe a point's neighborhood. Using a similarity metric with a density-based algorithm will cause a warning to be logged and the algorithm will fall back to the default separability metric (Euclidean distance).
Matrix imputation:
Pipeline:
Construct a pipeline of PreProcessors through which to push new data, resulting in a cluster fit:
// Unsupervised:
final KMedoidsParameters planner = new KMedoidsParameters(2).setVerbose(true);
// Use of varargs for the PreProcessors is supported
final UnsupervisedPipeline<KMedoids> pipe = new UnsupervisedPipeline<KMedoids>(planner, new StandardScaler() /*, ... */);
// Push data through preprocessing pipeline and fit model
KMedoids km = pipe.fit(mat);
// Supervised:
final NearestCentroidParameters s_planner = new NearestCentroidParameters().setVerbose(true);
final SupervisedPipeline<NearestCentroid> sup_pip = new SupervisedPipeline<NearestCentroid>(s_planner, new StandardScaler());
NearestCentroid model = sup_pip.fit(mat, new int[]{0,1,1});Note that normalization is recommended prior to clustering. Example on a KMeans constructor:
// For normalization, simply use a `PreProcessor`:
PreProcessor p = new StandardScaler().fit(X);
KMeans km = new KMeansParameters(k).fitNewModel(p.transform(X));By default, logging is disabled. This can be enabled by instance in any BaseClustererParameters class by invoking .setVerbose(true).
Note that the default setting may be set globally:
AbstractClusterer.DEF_VERBOSE = true;