Given an integer matrix, get the length of the longest increasing path.
https://leetcode.com/problems/longest-increasing-path-in-a-matrix/
Java Solution 1 – Naive DFS
public int longestIncreasingPath(int[][] matrix) { int[] max = new int[1]; for (int i = 0; i < matrix.length; i++) { for (int j = 0; j < matrix[0].length; j++) { dfs(matrix, i, j, max, 1); } } return max[0]; } public void dfs(int[][] matrix, int i, int j, int[] max, int len) { max[0] = Math.max(max[0], len); int m = matrix.length; int n = matrix[0].length; int[] dx = {-1, 0, 1, 0}; int[] dy = {0, 1, 0, -1}; for (int k = 0; k < 4; k++) { int x = i + dx[k]; int y = j + dy[k]; if (x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]) { dfs(matrix, x, y, max, len + 1); } } } |
This naive DFS solution’s time complexity is O(m*n*4^(m+n)).
Java Solution 2- Optimization with memorization
A common approach to improve DFS is through memorization.
public int longestIncreasingPath(int[][] matrix) { int result = 0; int m = matrix.length; int n = matrix[0].length; int[][] mem = new int[m][n]; for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { int t = helper(matrix, mem, i, j); result = Math.max(result, t); } } return result; } private int helper(int[][] matrix, int[][] mem, int i, int j) { if (mem[i][j] > 0) { return mem[i][j]; } int[] dx = {-1, 0, 1, 0}; int[] dy = {0, 1, 0, -1}; for (int k = 0; k < 4; k++) { int x = i + dx[k]; int y = j + dy[k]; if (x >= 0 && y >= 0 && x < matrix.length && y < matrix[0].length && matrix[x][y] > matrix[i][j]) { mem[i][j] = Math.max(mem[i][j], helper(matrix, mem, x, y)); } } return ++mem[i][j]; } |
Because of the memorization matrix, the upper bound time complexity of the DFS is O(m*n). With the loop in the main method, the overall time complexity is O(m^2 * n^2)
The following shows the first 4 elements’ DFS during iteration.
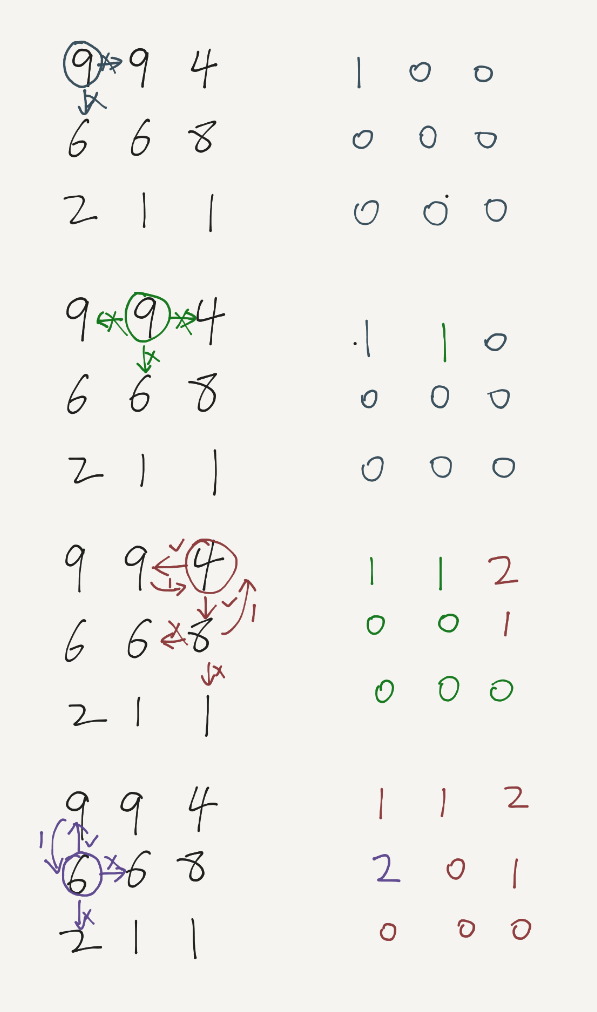
Explanation :- https://www.youtube.com/watch?v=xMa_zJAFn7o
Nope. The greater condition will take care of that.
Shouldn’t we track the visited coordinates?
that’s awesome solutions!