LeetCode – Count Complete Tree Nodes (Java)

by

Given a complete binary tree, count the number of nodes.

The solution to this problem can be as simple as the following:

public int countNodes(TreeNode root) {
    if(root == null){
        return 0;
    }
 
    return 1 + countNodes(root.left) + countNodes(root.right);
}

The following two solutions are improvements to this solution. The idea is that we can skip some elements to reduce time in the average case.

Java Solution 1

Steps to solve this problem:
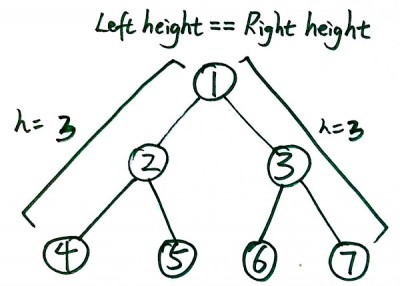
1) get the height of left-most part
2) get the height of right-most part
3) when they are equal, the # of nodes = 2^h -1
4) when they are not equal, recursively get # of nodes from left&right sub-trees

count-complete-tree-nodes

count-complete-tree-nodes-2

public int countNodes(TreeNode root) {
    if(root==null)
        return 0;
 
    int left = getLeftHeight(root)+1;    
    int right = getRightHeight(root)+1;
 
    if(left==right){
        return (2<<(left-1))-1;
    }else{
        return countNodes(root.left)+countNodes(root.right)+1;
    }
}
 
public int getLeftHeight(TreeNode n){
    if(n==null) return 0;
 
    int height=0;
    while(n.left!=null){
        height++;
        n = n.left;
    }
    return height;
}
 
public int getRightHeight(TreeNode n){
    if(n==null) return 0;
 
    int height=0;
    while(n.right!=null){
        height++;
        n = n.right;
    }
    return height;
}

Each time, you will have to do traversals along the left and right edges. At level h, you iterate zero times (no child). At level h – 1, you iterate once (one child). And so on. So that is 0 + 1 + 2 + … + h steps just to compute the left edges, which is h(1 + h)/2 = O(h^2).
The countNodes part has f(n) = 2 * 2 …* 2 = 2^h which is the number of nodes. Therefore, the time complexity is bounded by O(n) where n is the number of nodes in the tree.

Java Solution 2

public int countNodes(TreeNode root) {
    int h = getHeight(root);
    int total = (int)Math.pow(2, h)-1;
 
    //get num missed
    int[] miss = new int[1];
    helper(root, 0, h, miss);
 
    return total - miss[0];
}
 
//true continue, false stop
private boolean helper(TreeNode t, int level, int height, int[] miss){
    if(t!=null){
        level++;
    }else{
        return true;
    }
 
    if(level >=height){
        return false;
    }
 
    if(level == height-1){
        if(t.right == null){
            miss[0]++;
        }
        if(t.left == null){
            miss[0]++;
        }
 
        if(t.left!=null){
            return false;
        }
    }
 
    boolean r = helper(t.right, level, height, miss);
    if(r){
        boolean l = helper(t.left, level, height, miss);
        return l;
    }
 
    return true;
}
 
private int getHeight(TreeNode root){
    TreeNode p = root;
    int h = 0;
    while(p!=null){
        h++;
        p = p.left;
    }
    return h;
}

The sum of total node can also be written as:

int total = (2 << (h-1)) - 1;

Average time complexity is O(n/2), which is half of the number of nodes in the tree.

6 thoughts on “LeetCode – Count Complete Tree Nodes (Java)”

  1. recursive approach, may be it is expensive though but very easy and straight forward:
    it fails the online test saying time limit exceeded as it is visiting all the nodes so the optimal solution is up this is just a trivial one


    public int countNodes(TreeNode root) {

    if(root == null){
    return 0;
    }

    return 1 + countNodes(root.left) + countNodes(root.right);
    }

  2. if 6 is not in the tree in the first picture, then the tree will not be complete. Hence, will not be a complete binary tree.

  5. In the worst case, you will have to keep making recursive calls to the bottom-most leaf nodes (e.g. last level only have one single node). So you end up calling countNodes() h times. Each time, you will have to do traversals along the left and right edges. At level h, you iterate zero times (no child). At level h – 1, you iterate once (one child). And so on. So that is 0 + 1 + 2 + … + h steps just to compute the left edges, which is h(1 + h)/2 = O(h^2).

    The space complexity will just be the size of the call stack, which is O(h).

Leave a Comment