Problem:
Given a set of non-overlapping & sorted intervals, insert a new interval into the intervals (merge if necessary).
Example 1: Given intervals [1,3],[6,9], insert and merge [2,5] in as [1,5],[6,9]. Example 2: Given [1,2],[3,5],[6,7],[8,10],[12,16], insert and merge [4,9] in as [1,2],[3,10],[12,16]. This is because the new interval [4,9] overlaps with [3,5],[6,7],[8,10].
Java Solution 1
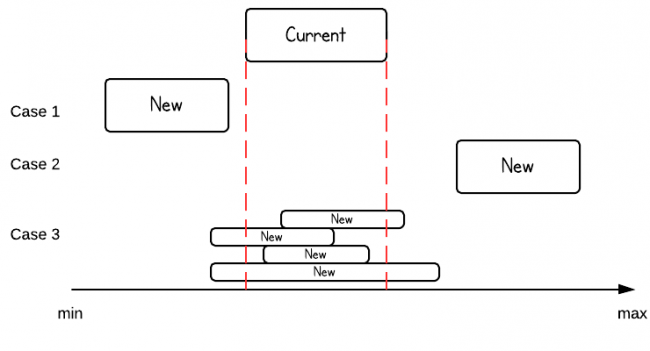
When iterating over the list, there are three cases for the current range.
/** * Definition for an interval. * public class Interval { * int start; * int end; * Interval() { start = 0; end = 0; } * Interval(int s, int e) { start = s; end = e; } * } */ public class Solution { public ArrayList<Interval> insert(ArrayList<Interval> intervals, Interval newInterval) { ArrayList<Interval> result = new ArrayList<Interval>(); for(Interval interval: intervals){ if(interval.end < newInterval.start){ result.add(interval); }else if(interval.start > newInterval.end){ result.add(newInterval); newInterval = interval; }else if(interval.end >= newInterval.start || interval.start <= newInterval.end){ newInterval = new Interval(Math.min(interval.start, newInterval.start), Math.max(newInterval.end, interval.end)); } } result.add(newInterval); return result; } } |
Java Solution 2 – Binary Search
If the intervals list is an ArrayList, we can use binary search to make the best search time complexity O(log(n)). However, the worst time is bounded by shifting the array list if a new range needs to be inserted. So time complexity is still O(n).
public List<Interval> insert(List<Interval> intervals, Interval newInterval) { List<Interval> result = new ArrayList<>(); if (intervals.size() == 0) { result.add(newInterval); return result; } int p = helper(intervals, newInterval); result.addAll(intervals.subList(0, p)); for (int i = p; i < intervals.size(); i++) { Interval interval = intervals.get(i); if (interval.end < newInterval.start) { result.add(interval); } else if (interval.start > newInterval.end) { result.add(newInterval); newInterval = interval; } else if (interval.end >= newInterval.start || interval.start <= newInterval.end) { newInterval = new Interval(Math.min(interval.start, newInterval.start), Math.max(newInterval.end, interval.end)); } } result.add(newInterval); return result; } public int helper(List<Interval> intervals, Interval newInterval) { int low = 0; int high = intervals.size() - 1; while (low < high) { int mid = low + (high - low) / 2; if (newInterval.start <= intervals.get(mid).start) { high = mid; } else { low = mid + 1; } } return high == 0 ? 0 : high - 1; } |
The best time is O(log(n)) and worst case time is O(n).
O(log n) solution using Binary Search from the left and right sides,, but the worst case is still O(n) due to existing of shifting the whole intervals case
class Solution {
public:
vector mergeIntervals(vector l1, vector l2) {
vector l(2);
l[0] = min(l1[0], l2[0]);
l[1] = max(l1[1], l2[1]);
return l;
}
vector<vector> insert(vector<vector>& intervals, vector& newInterval) {
vector<vector> ans;
/* handle base case */
if(intervals.empty()) {
ans.push_back(newInterval);
return ans;
}
int firstNonOverlappedFromLeft = -1, firstNonOverlappedFromRight = intervals.size();
/* find first non overlapped interval from left side */
int L = 0, R = intervals.size() - 1;
while(L <= R) {
int mid = (L + R) / 2;
if(intervals[mid][1] < newInterval[0]) {
firstNonOverlappedFromLeft = mid;
L = mid + 1;
}
else {
R = mid - 1;
}
}
/* find first non overlapped interval from right side */
L = 0, R = intervals.size() - 1;
while(L newInterval[1]) {
firstNonOverlappedFromRight = mid;
R = mid - 1;
}
else {
L = mid + 1;
}
}
/* merge the ovelapped intervals with each other */
int ind = 0;
while(ind <= firstNonOverlappedFromLeft) ans.push_back(intervals[ind++]);
ans.push_back(newInterval);
while(ind < firstNonOverlappedFromRight)
ans[firstNonOverlappedFromLeft + 1] = mergeIntervals(ans[firstNonOverlappedFromLeft + 1], intervals[ind++]);
while(ind < intervals.size()) ans.push_back(intervals[ind++]);
return ans;
}
};
First thing that came to mind is binary search. I wonder admin considered it to be unnecessarily complex or something.
I propose a best case O(log N) solution based on binary search. Note however that the overall algorithm can have a O(N) cost due to interval removal from the array (cost of arbitrary position removal in an array) – which could be optimized/amortized separately.
class Interval {
final int s;
final int e;
Interval(int s, int e) { this.s = s; this.e = e; }
/** Assumes there exists an overlap */
Interval merge(Interval o) {
return new Interval(Math.min(s, o.s), Math.max(e, o.e));
}
}
void insert(Interval i, ArrayList sortedList) {
if (sortedList.isEmpty()) {
sortedList.add(i);
return;
}
int idxS = searchInsertIdx(i.s, sortedList);
//we look for e+1 because we want to merge if eq too (see logic later)
int idxE = searchInsertIdx(i.e + 1, sortedList);
boolean replaceS = false;
if (idxS > 0) {
Interval prev = sortedList.get(idxS - 1);
if (prev.e >= i.s) {
i = i.merge(prev);
idxS -= 1;
replaceS = true;
}
}
if (idxS < idxE) {
Interval lastToMerge = sortedList.get(idxE - 1);
i = i.merge(lastToMerge);
if ((idxS + 1) < idxE) {
removeRange(idxS + 1, idxE, sortedList);
replaceS = true;
}
}
if (replaceS) sortedList.set(idxS, i);
else sortedList.add(idxS, i);
}
void removeRange(int s, int e, ArrayList sortedList) {
sortedList.subList(s, e).clear();
}
/* Returns the position where an Interval starting at startValue should be inserted ignoring merges */
int searchInsertIdx(int startValue, ArrayList sortedList) {
if (sortedList.isEmpty()) return 0;
int s = 0;
int e = sortedList.size();
while (e > s) {
int mid = (e + s)/2;
Interval atMid = sortedList.get(mid);
if (atMid.s == startValue) return mid;
else if(atMid.s < startValue) s = mid + 1;
else e = mid - 1;
}
return sortedList.get(s).s < startValue? s + 1 : s;
}
sortmerge
It’s a great solution. I think this is not necessary, though:
|| interval.start <= newInterval.end
just add the new interval, and run 7) Merge Intervals
I add some check before inserting. Sorry, attached pic twice. Don’t know how to remove it.
public class Solution {
public ArrayList insert(ArrayList intervals, Interval newInterval) {
ArrayList ans = new ArrayList();
int size = intervals.size();
while( size > 0 ) {
Interval i = intervals.remove(0);
size–;
if( i.end < newInterval.start )
ans.add( i );
else if ( newInterval.end < i.start ) {
ans.add( newInterval );
ans.add( i );
ans.addAll( intervals );
return ans;
} else {
newInterval.start = Math.min( newInterval.start, i.start );
newInterval.end = Math.max( newInterval.end, i.end );
}
}
ans.add( newInterval );
return ans;
}
Is there any typo in this solution. It doesn’t work.